It's Actors All The Way Down

A classic problem in concurrent programming is known as the “same fringe” problem [1]. What is the same fringe problem? As described by Richard Gabriel [2]:

The samefringe problem is this: two binary trees have the same fringe if they have exactly the same leaves reading from left to right.

There are many different approaches to solving this problem in a variety of languages. Our approach is to incrementally generate a stream of leaves from a tree (the fringe). We will use a comparison process to read from a pair of streams (one for each tree) and report if they are the same or different. Comparison stops as soon as we detect a difference, avoiding the need to generate the rest of the fringe.

Stream Generators

When we generate the fringe of a tree, we follow a stream-generator protocol. Before we get into the fringe itself, let’s examine a protocol for streams in general.

A stream-generator receives requests with only a customer. It sends a pair to this customer consisting of a value and an actor to ask for the next pair. You can think of the actor as representing a position in the stream.

A simple stateful stream-generator is one that generates an infinite sequence of values.

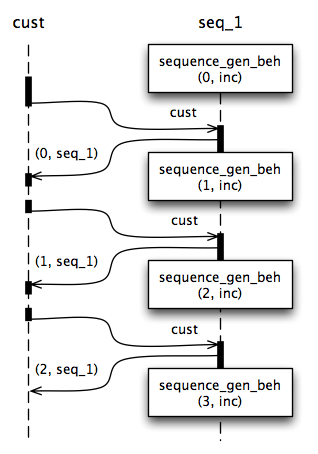
LET sequence_gen_beh(value, fn) = \cust.[
	BECOME sequence_gen_beh(fn(value), fn)
	SEND (value, SELF) TO cust
]

The sequence begins with an initial value. When a request is received designating a customer cust, the mutable state of the stream is updated by applying a function fn to the value. The customer is sent a pair consisting of the original value and a reference to itself. Since its state has been updated with the new value, the actor to ask for the next value is the same actor.

Figure 1 - Mutable Stream-Generator

We can also generate the same sequence of values using immutable actors.

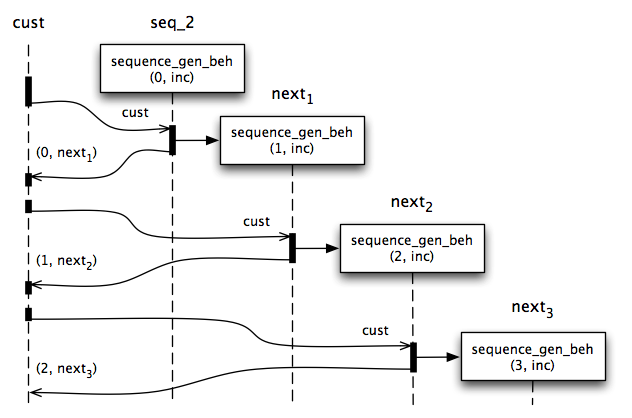
LET sequence_gen_beh(value, fn) = \cust.[
	CREATE next WITH sequence_gen_beh(fn(value), fn)
	SEND (value, next) TO cust
]

In this implementation, rather than altering the state of the current actor, we create a new actor to represent the next value in the sequence. This allows us to retain references to actors representing any particular position in the stream and ask them to replay the stream from that position.

Figure 2 - Immutable Stream-Generator

The immutable implementation can be made more efficient by avoiding recalculation of successive values when the sequence is replayed.

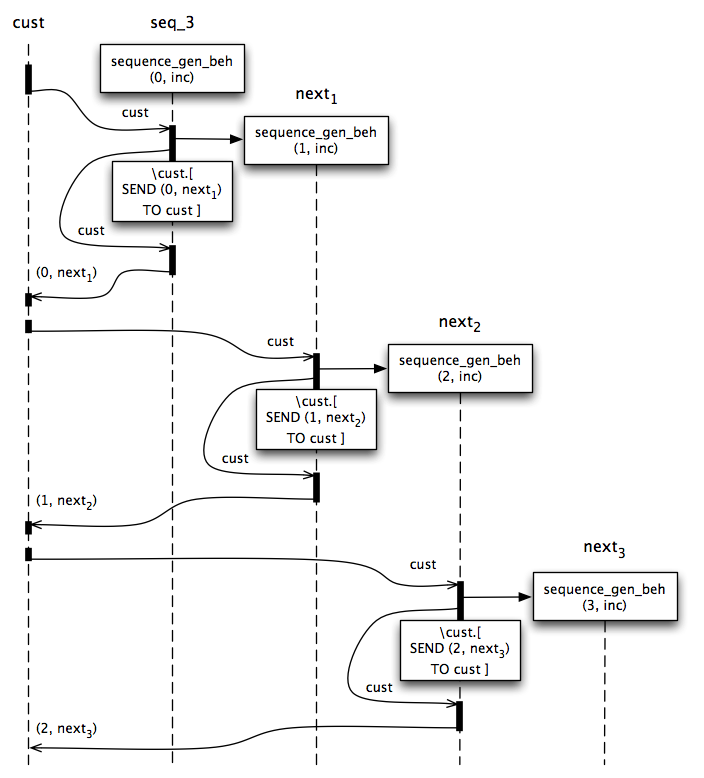
LET sequence_gen_beh(value, fn) = \cust.[
	CREATE next WITH sequence_gen_beh(fn(value), fn)
	BECOME \cust.[
		SEND (value, next) TO cust
	]
	SEND cust TO SELF
]

In this implementation, we only calculate the next value once. We change the actor’s subsequent behavior to always return the same value and next. We re-issue the request (the customer cust) to the updated actor. This is a form of memoization. Once initialized, each actor is immutable.

Figure 3 - Memoizing Stream-Generator

Notice that all of these actor behaviors support the same protocol. From the perspective of a customer reading the stream only once, their observable behavior is identical. The mutable and immutable versions differ in their handling of repeated requested to the same actor. Specifically, the mutable version is not re-usable since it becomes the representation of the next position on each request.

Fringe Generation

The fringe generator produces a stream of values, pairing each value with an actor representing the generator of the next value. Each fringe generator actor maintains a location in the tree, and the actor that will generate the next result. By convention, when next is NIL, we’ve reached the end of the stream. The generator has mutable state. It is intended to be used only once.

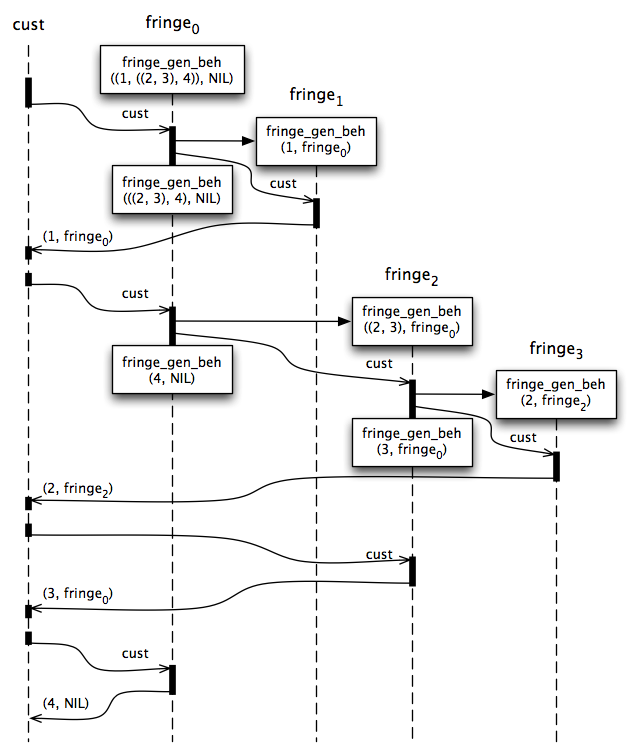
LET fringe_gen_beh(tree, next) = \cust.[
	IF $tree = (left, right) [
		SEND cust TO NEW fringe_gen_beh(left, SELF)
		BECOME fringe_gen_beh(right, next)
	] ELSE [
		SEND (tree, next) TO cust
	]
]

When a customer cust requests a value, we check if tree is a branch or a leaf. If we have a leaf, we send the customer the leaf value tree and the next actor. If we have a branch, we create an actor to represent the left part of the tree, designating the current actor as next. We send the customer cust to the new actor in order to process the left sub-tree first. The current actor becomes the representation of the right part of the tree, using the original value of next. In this way, once the left sub-tree has been processed, the right sub-tree is processed as next. Once the right sub-tree has been processed, we continue with the original next.

Figure 4 - Fringe Stream-Generator

Figure 4 illustrates the fringe 1, 2, 3, 4 generated from the tree (1, ((2, 3), 4)). Note how the fringe is generated incrementally. Each request only does enough work to locate the next element of the fringe. This property is critical to the efficient comparison of trees with large fringe, especially if they differ in the early part of the fringe.

Stream Comparison

Checking two trees for the same fringe is accomplished by comparing corresponding values from two fringe-generator streams. We create an actor behavior for incrementally comparing two streams regardless of how they are generated.

LET cmp_stream_beh(cust) = \(value, next).[
	BECOME \(value', next').[
		IF $value = $value' [
			BECOME cmp_stream_beh(cust)
			IF $next = $next' [
				SEND TRUE TO cust
			] ELIF $next = NIL [
				SEND FALSE TO cust
			] ELIF $next' = NIL [
				SEND FALSE TO cust
			] ELSE [
				SEND SELF TO next
				SEND SELF TO next'
			]
		] ELSE [
			SEND FALSE TO cust
		]
	]
]

The stream comparison actor is designed to be used as the customer for two stream-generators. It maintains its own customer cust to report a TRUE orFALSE comparison result. When it receives a value and next from one of the streams, it transitions to a state waiting for the other stream. It doesn’t matter which stream generates a value first. When a value’ and next’ is received from the other stream, we now can compare corresponding values. If the values don’t match, we send FALSE to the original customer cust. We only read enough of each stream to locate their first difference, or keep reading (as long as they match) until they both end.

If the values match, we prepare to receive (and compare) another set of corresponding values. However, before we can ask each generator to generate their next values, we have to check for termination conditions. If next and next’ match (usually because both are NIL), we send TRUE to the original customer cust, since we’ve successfully matched everything up through the end of both streams. If either next or next’ are NIL, we send FALSE to the original customer cust, since one stream has ended before the other. Otherwise, we send the comparison actor (our SELF) to each stream, requesting the next value from each.

Using these building blocks, we can create a service to compare pairs of trees.

CREATE same_fringe_svc WITH \(cust, a, b).[
	CREATE match WITH cmp_stream_beh(cust)
	SEND match TO NEW fringe_gen_beh(a, NIL)
	SEND match TO NEW fringe_gen_beh(b, NIL)
]

The service creates a new stream comparison process match that reports its results to the customer cust. A fringe generator is created for each tree. The comparator match is sent (as a customer) to both streams, initiating the process of reading and comparing corresponding values from each stream.

The following test case generates a TRUE result:

LET a = (1, ((2, 3), 4))
LET b = ((1, (2, 3)), 4)
SEND (println, a, b) TO same_fringe_svc

The following test case generates a FALSE result:

LET a = (1, ((2, 3), 4))
LET z = (1, 0, 3, 4)
SEND (println, a, z) TO same_fringe_svc

An important property of the stream comparison process is that it avoids reading beyond the point of difference between the streams. This is especially important if one of the streams is infinite. Consider the result of executing the following:

LET a = (1, ((2, 3), 4))
CREATE match WITH cmp_stream_beh(println)
SEND match TO NEW fringe_gen_beh(a, NIL)
SEND match TO NEW sequence_gen_beh(1, inc)

The sequence generator will produce an infinite sequence starting with 1, 2, 3, 4... (assuming that inc is an integer increment function). The fringe generator will produce the same initial values, but ends after 4. The stream comparison process will report FALSE after the fourth value and stop reading the streams.

Conclusion

The “same fringe” problem is considered one of the simplest problems that requires concurrency to implement efficiently. It seems to require a non-deterministic merge between two incrementally-generated streams of information. Asynchronous actor messaging provides the means for handling the non-deterministic merge (comparison). In addition, this problem provides an excellent illustration of the use of incremental stream generators. We will have much more to say about stream-based processing in future articles.

References

[1]

C. Hewitt, et. al. Behavioral Semantics of Non-recursive Control Structures, Proc. Colloque sur la Programmation, B. Robinet ed., in Lecture Notes in Computer Science, No. 19, Springer Verlag, 1974.

[2]

R. Gabriel. The Design of Parallel Programming Languages. http://www.dreamsongs.com/10ideas.html, 1991.