It's Actors All The Way Down

A Finger Tree is a data-structure that supports amortized O(1) addition and removal of elements from either end [1]. It also can support a large number of common sequence operations, including concatenation, very efficiently. Our implementation is based on the Hinze-Paterson structure [2], simplified for use as a Deque. It is possible to implement a Finger Tree in Humus using pure functions, like most traditional implementations. However, the implementation shown here uses an object-oriented approach instead.

This will be the first blog post that doesn’t use actors in the implementation. Since we are working with value objects, there is no mutable state, thus no need for actors. However, Finger Trees do provide a safe immutable value type which can be passed in messages and safely shared among actors, so they are quite useful in an actor context. On another level, as previously discussed, actors can be used to evaluate arbitrarily complex/recursive functions (like those used to implement Finger Trees) without blocking the rest of the system.

Value Objects

An object combines data with methods that operate on that data. Generally, objects have mutable state, which may be changed by methods of the object. A value object is an immutable object. Object methods may access the object state, but do not change it. Object methods are associated with each instance, so the same method name may select a different implementation on a different object. This is known as polymorphism. Humus does not have any special syntax for object methods calls. Instead, we make method dispatch explicit by defining a function that makes a method call on our value-objects.

LET vo_call(this, req) = (
	LET (vo, _) = $this
	IN vo(this, req)
)

Our value-object representation is a tuple with two or more elements, where the first element is a function that dispatches object methods. Our objects are polymorphic, but they are not encapsulated. Their state is not protected from direct access. However, this will suffice for our purposes.

The vo_call function extracts the dispatch function vo from the object this. The dispatch function is applied to the object and the original request req. The result of this function call is the value returned.

Fingers

Before we can build a Finger Tree, we need to define the Fingers which represent prefix and suffix segments of the tree. There are four types of fingers, storing one, two, three or four elements respectively. Let’s consider the dispatch function for a one-finger value object.

LET 1F = \(this, req).(
	LET ($1F, a) = $this IN
	CASE req OF
	(#put, x) : (2F, a, x)
	(#push, x) : (2F, x, a)
	END
)

First, the dispatch function ensures that the object passed as this has the correct structure for a one-finger. Specifically, a tuple starting with the dispatch function 1F and holding a data element. If the structure is correct, then the request req is matched with the supported operations, #put and #push. The result of #put is a new two-finger holding the original element a and the new element x. Similarly, #push creates a two-finger, but with the new element before the original.

Fingers can not be empty, so the one-finger does not support any operations which remove elements. The two-finger, on the other hand, supports the full Deque protocol.

LET 2F = \(this, req).(
	LET ($2F, a, b) = $this IN
	CASE req OF
	(#put, x) : (3F, a, b, x)
	(#pop) : (a, (1F, b))
	(#push, x) : (3F, x, a, b)
	(#pull) : (b, (1F, a))
	END
)

The #put and #push operations create a new three-finger, with the new element at the end/beginning respectively. The #pop and #pull operations return the first/last element respectively, and a new one-finger holding the one element remaining.

The three-finger and four-finger object types follow the same pattern. Note that the four-finger does not support operations which add elements, because it is largest finger type.

LET 3F = \(this, req).(
	LET ($3F, a, b, c) = $this IN
	CASE req OF
	(#put, x) : (4F, a, b, c, x)
	(#pop) : (a, (2F, b, c))
	(#push, x) : (4F, x, a, b, c)
	(#pull) : (c, (2F, a, b))
	END
)

LET 4F = \(this, req).(
	LET ($4F, a, b, c, d) = $this IN
	CASE req OF
	(#pop) : (a, (3F, b, c, d))
	(#pull) : (d, (3F, a, b, c))
	END
)

Finger Trees

There are three types of Finger Trees, empty, singleton and full. Empty is, of course, the simplest case.

LET 0T = \(this, req).(
	CASE req OF
	(#put, x) : (ST, x)
	(#push, x) : (ST, x)
	END
)
LET EMPTY = $(0T, NIL)

The empty tree has no data and, since it is immutable, a single EMPTY instance can be shared by all. Figure 1 shows a Finger Tree initialized with a reference to EMPTY.

Figure 1 – Empty Tree

The empty tree, naturally, does not support removal of elements. Addition of an element creates a new singleton tree which holds the element. Figure 2 shows the singleton tree holding the symbol A after a #put.

Figure 2 – Singleton Tree

A singleton tree stores a single element and supports the full Deque protocol.

LET ST = \(this, req).(
	LET ($ST, v) = $this IN
	CASE req OF
	(#put, x) : (FT, (1F, v), (EMPTY), (1F, x))
	(#pop) : (v, (EMPTY))
	(#push, x) : (FT, (1F, x), (EMPTY), (1F, v))
	(#pull) : (v, (EMPTY))
	END
)

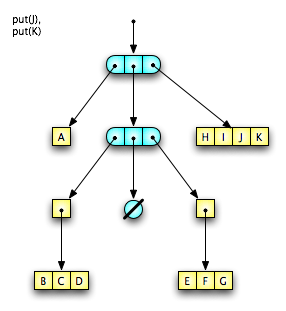
Unlike a one-finger object, elements can be removed from a singleton tree, resulting in the empty tree. Also, when an element is added, a full tree is created instead of a two-finger. Figure 3 shows the full tree holding the symbols A and B after a #put on the singleton tree from Figure 2.

Figure 3 – A-B Finger Tree

A full tree consists of a prefix-finger, a suffix-finger and a middle tree. Figure 3 shows a minimal full tree, with a one-finger prefix, a one-finger suffix, and an empty middle tree. The full-tree implementation is a little more complex, so we’ll start by considering only the #put operation, which returns the Finger Tree that results from adding an element at the end of the sequence.

LET FT = \(this, req).(
	LET ($FT, p, q, r) = $this IN
	CASE req OF
	(#put, x) : (
		IF $r = ($4F, a, b, c, d) (
			LET q' = $vo_call(q, #put, (3F, a, b, c))
			IN (FT, p, q', (2F, d, x))
		) ELSE (
			(FT, p, q, vo_call(r, #put, x))
		)
	)
	...
	END
)

The #put operation has to handle two cases based on whether the suffix-finger r is full or not. If the suffix-finger has less than four elements, then there is room to put another element into the finger. This is done by calling #put on the finger. Figure 4 shows the result of doing this three times, resulting in a full four-finger suffix.

Figure 4 – A-E Finger Tree

When the suffix-finger is full, and we #put another element, we gather the first three elements of the suffix into a three-finger and #put it into the middle tree, and a new two-finger suffix is created from the fourth element and the new element. Since the middle tree is currently empty in this case, it responds to the #put by creating a singleton tree, as shown in Figure 5.

Figure 5 – A-F Finger Tree

After #put-ing two more elements, the suffix-finger is full again, as shown in Figure 6.

Figure 6 – A-H Finger Tree

Figure 7 shows the restructuring that results from #put-ing the ninth element into the tree. Notice that the elements managed at the second-level of depth in the tree are fingers, not just data elements. We saw this first in Figure 6, where a singleton referred to a three-finger value. Now, when the next three-finger propagates into the middle tree, the singleton is replaced by a full tree. However, in trees at this level, the elements are themselves fingers, so we have a one-finger prefix and a one-finger suffix, both referring to three-finger values.

Figure 7 – A-I Finger Tree

Two more elements #put again re-fill the top-level suffix-finger, as shown in Figure 8.

Figure 8 – A-K Finger Tree

Element twelve once again propagates a three-finger into the middle tree, but this time it simply makes a two-finger suffix at the next level in the tree, as shown in Figure 9.

Figure 9 – A-L Finger Tree

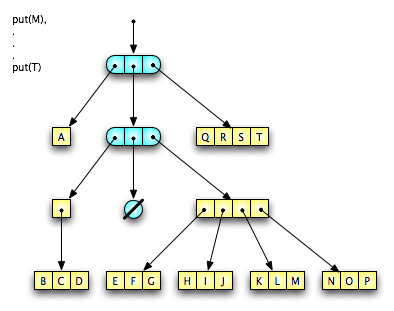
It takes twenty elements #put before two levels of suffix-fingers are filled, as shown in Figure 10. Notice how little work is done to continue expanding the sequence held by the tree. Two-thirds of the elements #put are handled directly by the top-level suffix-finger. One out of every three elements #put causes a three-finger to propagate into the middle tree. Each level of the tree manages larger and larger sub-structures, further reducing the work required to keep the tree properly organized.

Figure 10 – A-T Finger Tree

Figure 11 shows how this pattern continues to the third level of depth, with the #put of element twenty-one. When the second-level suffix is full, a three-finger is created as before, but this time the elements are themselves three-fingers. The previously empty second-level middle tree is replaced by a singleton tree holding this compound finger value.

Figure 11 – A-U Finger Tree

We have shown how the Finger Tree structure can be built up by incremental addition of elements. Now let’s consider element removal. Specifically, we will focus on the #pop operation, which returns a tuple consisting of the item previously at the beginning of the sequence, and the new Finger Tree resulting from the removal.

LET FT = \(this, req).(
	LET ($FT, p, q, r) = $this IN
	CASE req OF
	...
	(#pop) : (
		IF $p = ($1F, a) (
			IF $q = ($EMPTY) (
				IF $r = ($1F, x) (
					(a, (ST, x))
				) ELSE (
					LET (x, r') = $vo_call(r, #pop)
					IN (a, (FT, (1F, x), q, r'))
				)
			) ELSE (
				LET (p', q') = $vo_call(q, #pop)
				IN (a, (FT, p', q', r))
			)
		) ELSE (
			LET (x, p') = $vo_call(p, #pop)
			IN (x, (FT, p', q, r))
		)
	)
	...
	END
)

There are four cases to consider. If the tree is minimal (one-finger prefix, empty middle, one-finger suffix), then #pop produces a singleton tree holding the remaining element.

If there is a one-finger prefix, an empty middle, and more than one element in the suffix, then one element is #pop-ed from the suffix and used to create a new one-finger prefix.

If there is a one-finger prefix, and the middle is not empty, then one element is #pop-ed from the middle and becomes the new prefix.

Finally, if there is more than one element in the prefix, then one element is #pop-ed from the prefix and the prefix is updated. This is the least amount of work, and is the case that accounts for two-thirds of the #pop operations.

Figure 12 – B-U Finger Tree after “pop”

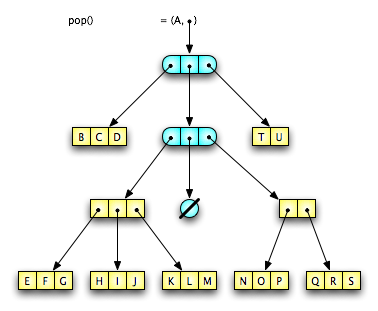
Figure 12 shows the result of a #pop operation on the Finger Tree from Figure 11. Notice how only a few internal nodes had to change to accomplish a relatively deep restructuring. As was true with element addition, element removal usually requires very few operations, with restructuring required more and more rarely as you go deeper into the tree.

The #push and #pull operations, which round out the rest of the Deque protocol, are mirror images of #put and #pop. If you’ve understood the code so far, the rest should be straight-forward.

LET FT = \(this, req).(
	LET ($FT, p, q, r) = $this IN
	CASE req OF
	...
	(#push, x) : (
		IF $p = ($4F, a, b, c, d) (
			LET q' = $vo_call(q, #push, (3F, b, c, d))
			IN (FT, (2F, x, a), q', r)
		) ELSE (
			(FT, vo_call(p, #push, x), q, r)
		)
	)
	(#pull) : (
		IF $r = ($1F, a) (
			IF $q = ($EMPTY) (
				IF $p = ($1F, x) (
					(a, (ST, x))
				) ELSE (
					LET (x, p') = $vo_call(p, #pull)
					IN (a, (FT, p', q, (1F, x)))
				)
			) ELSE (
				LET (r', q') = $vo_call(q, #pull)
				IN (a, (FT, p, q', r'))
			)
		) ELSE (
			LET (x, r') = $vo_call(r, #pull)
			IN (x, (FT, p, q, r'))
		)
	)
	END
)

The last three code fragments should be combined into a single FT definition, giving you the dispatch function for a full Finger Tree value-object.

Conclusion

We have shown how to implement a Finger Tree using a transparent representation of functional value-objects. This versatile and efficient immutable data-structure can be safely shared among collaborating actors. Operations on the tree produce a new tree that shares as much structure and data as possible with the old tree, without disturbing the old structure. This allows effortless versioning, since all previous versions remain available as long as there are references to them. Unreferenced versions are automatically reclaimed by garbage-collection.

References

[1]

C. Okasaki. Purely Functional Data Structures. Cambridge University Press, 1998.

[2]

R. Hinze, R. Paterson. Finger Trees: A Simple General-purpose Data Structure. Journal of Functional Programming, 16(2):197–217, 2006.