Deconstructing the Actor Model
The Actor Model of Computation, as defined by Carl Hewitt [1] and elaborated by Gul Agha [2], defines three primitive operations. These operations are “Send”, “Create” and “Become”. The “Send” operation transmits an asynchronous message to a known receiver. The “Create” operation constructs a new actor with a specified initial behavior. The “Become” operation defines the behavior used to process the next message received by the current actor. We will examine each of these primitives, focusing on their relationship with various computational concepts. The actor model provides a compact mode of expression. By unpacking this model, we hope to better understand how to take advantage of its power and elegance.
Actor processing is triggered by receiving a message, thus actors are described as concurrent reactive processing elements. The behavior of an actor defines the operations it performs when a message is received. In response to a message, an actor may:
- send a finite number of new messages
- create a finite number of new actors
- designate a new behavior to process subsequent messages
If a new behavior is not specified, the current behavior will be used to process the next message received. Each received message is processed serially. The next message cannot be received until the behavior processing the current message determines the behavior for processing subsequent messages. This is the intrinsic mechanisms of actor concurrency control. Messages may be delivered concurrently to different actors, but each actor processes messages one-at-a-time.
Send Message
The “Send” primitive transmits a value from the current actor to a receiving actor. The receiving actor is designated by an opaque value that uniquely identifies the actor. The message is sent asynchronously. The sender does not “wait” for the message to be received. There is no indication to the sender when the message was received, although the receiver may send another message as a reply. The receiving actor does not know the identity of the sender, unless the sender explicitly includes their own identity in the message. Each actor knows it’s own identity. It may also know the identity of other actors either given to it at creation time or received in earlier messages.
Let’s examine the implications of asynchronous message sending. We’ll start with a traditional example, calculation of a factorial. First, we’ll create an actor that will serve as a factorial service.
CREATE fact_svc WITH \(cust, acc, n).[ IF $n = 0 [ SEND acc TO cust ] ELSE [ SEND (cust, mul(acc, n), sub(n, 1)) TO SELF ] ]
This creates a new actor and binds it to the fact_svc variable. The behavior of this actor expects a 3-tuple consisting of a customer, an accumulated value, and a number. If the number n is zero, the value of the accumulator acc (initially one) is sent to the customer cust. Otherwise, a new 3-tuple message is constructed with the original cust, acc × n, and n − 1. This message is sent back to fact_svc via the SELF keyword.
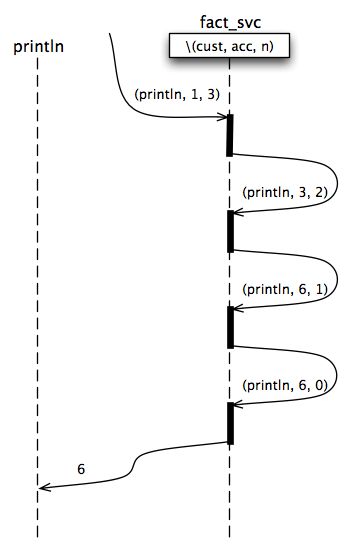
We can calculate the factorial of 3 (see Figure 1) with a message like this:
SEND (println, 1, 3) TO fact_svc
We assume the existence of a println actor that displays any message it receives. We will use println as the customer, in order to display the final result of the computation. When the initial message is received by fact_svc, since n is 3, the message (println, 3, 2) is sent back to fact_svc. On receiving this message, since n is 2, the message (println, 6, 1) is sent back to fact_svc. On receiving this message, since n is 1, the message (println, 6, 0) is sent back to fact_svc. On receiving this message, since n is 0, the final result 6 is sent to println. While this may not be optimal computationally, it does result in the computation of 6 as the factorial of 3.
Note that the factorial service is completely stateless. Messages from multiple overlapping factorial computations can be safely interleaved without interfering with each other. Each message represents a work-step, and carries with it all of the information needed to perform the next step of the process.
Create Actor
The “Create” primitive constructs a new actor with a specified initial behavior. This primitive allows an actor configuration to grow and change. The identity of the newly-created actor is made available to the actor that created it. If this identity is not shared, it will remain known only to the creator. Actor identities can be used as security capabilities. Actor identities can also be transmitted in messages. Any actor that knows another actor’s identity may send a message to that actor.
Actor creation is very inexpensive in both storage and execution time. Therefore, it can be used to efficiently maintain temporary state during a computation. Consider this alternate implementation of a factorial service. The fact_acc behavior is used to create actors that hold partial results.
LET fact_acc(cust, n) = \m.[ SEND mul(m, n) TO cust ] CREATE fact_svc WITH \(cust, n).[ IF $n = 0 [ SEND 1 TO cust ] ELSE [ CREATE acc WITH fact_acc(cust, n) SEND (acc, sub(n, 1)) TO SELF ] ]
The behavior of this actor expects a pair consisting of a customer and a number. If the number n is zero, one is sent to the customer cust. Otherwise, a new actor acc is created to accumulate the multiplications of the factorial. This accumulator is used as the customer for a new request to compute the factorial of n − 1. The accumulator actor is like a stack-frame that might be created during calls to a recursive functional implementation of factorial. It holds the value to be multiplied once the next-lower factorial value is returned. The recursion terminates when n = 0 and the value 1 is returned. This triggers a chain of customers, each multiplying the accumulated value m by the number it saved n, until the original customer is sent the final value.
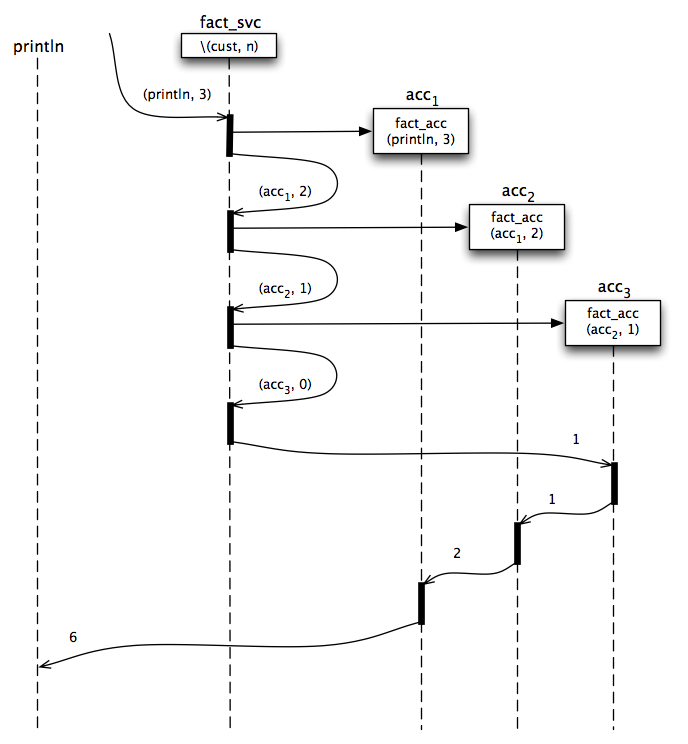
Let consider again calculating the factorial of 3 (see Figure 2) with a message like this:
SEND (println, 3) TO fact_svc
When the initial message is received by fact_svc, since n is 3, a new actor acc1 is created with a behavior of fact_acc(println, 3), and the message(acc1, 2). is sent back to fact_svc. On receiving this message, since n is 2, a new actor acc2 is created with a behavior of fact_acc(acc1, 2), and the message (acc2, 1). is sent back to fact_svc. On receiving this message, since n is 1, a new actor acc3 is created with a behavior of fact_acc(acc2, 1), and the message (acc3, 0). is sent back to fact_svc. On receiving this message, since n is 0, the value 1 is sent to acc3. On receiving this message, acc3computes 1 × 1 = 1, and sends 1 to acc2. On receiving this message, acc2 computes 1 × 2 = 2, and sends 2 to acc1. On receiving this message, acc1computes 2 × 3 = 6, and sends 6 to println, the original customer.
This version of the factorial service is still stateless. Partial results are captured by the creation of temporary “accumulator” actors which maintain the computational state. While this is not strictly neccessary in the case of the factorial computation, it serves to illustrate how the state of a computation can be represented through actor creation. It also illustrates a mechanism of implementing recursive stack-frames that hold intermediate values.
Become Behavior
The “Become” primitive specifies the behavior that will be used to process the next message received by the current actor. If no replacement behavior is specified, the current behavior will be used to process the next message. “Become” is the state-changing primitive. The state of an actor is represented by the actor’s response to messages, thus changing an actor’s behavior changes its apparent state. If an actor’s behavior does not contain a “Become”, it is effectively stateless.
A simple numeric counter will serve to illustrate concurrent access to shared state. First, we’ll define a function that creates a behavior value for a counter.
LET counter_beh(value) = \(cust, req).[ CASE req OF #get : [ SEND value TO cust ] (#set, value') : [ BECOME counter_beh(value') SEND value' TO cust ] (#inc, amount) : [ LET value' = $(add(value, amount)) BECOME counter_beh(value') SEND value' TO cust ] END ]
Behaviors created by this function have a known value and process requests matching three distinct patterns. A message like (println, #get) will send the current value to the customer println (which displays the value). A message like (println, #set, 1) will assign a new behavior (with a value of 1) to the current actor, and send the new value to the customer. A message like (println, #inc, 1) compute a new value by adding amount to the current value, assign a new behavior (with the new value) to the current actor, and send the new value to the customer.
Next, we create a counter with an initial value of zero.
CREATE counter_0 WITH counter_beh(0)
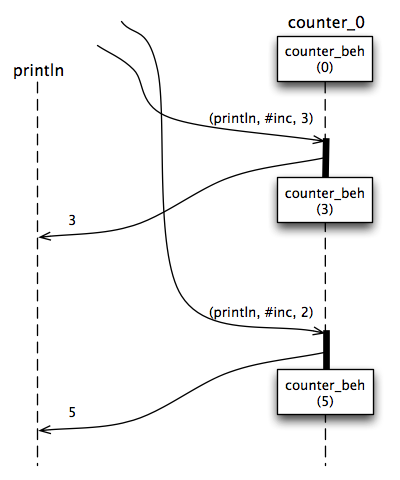
Now we send a couple of message to counter_0
SEND (println, #inc, 2) TO counter_0 SEND (println, #inc, 3) TO counter_0
The display will now show either:
2 5
or (as shown in Figure 3)
3 5
depending on which increment request is processed first. The requests are each processed atomically, but they may be received in either order. Note that the state is always consistently maintained. Each state-changing operation determines a new behavior that represented the updated state, and that behavior is used to process subsequent messages.
We can expose the effects of actor concurrency management by considering this dangerous definition for the behavior of a counter.
LET bad_counter_beh(value) = \(cust, req).[ CASE req OF #get : [ SEND value TO cust ] (#set, value') : [ BECOME bad_counter_beh(value') SEND (cust, #get) TO SELF ] (#inc, amount) : [ LET value' = $(add(value, amount)) SEND (cust, #set, value') TO SELF ] END ]
This implementation has factored out some common parts of the behavior. When a #set request is handled, it updates the behavior to reflect the new state, but then delegates to its own handling of #get to send the updated value back to the customer. When an #inc request is handled, it computes the new value, but then delegates to its own handling of #set to apply the update and reply to the customer.
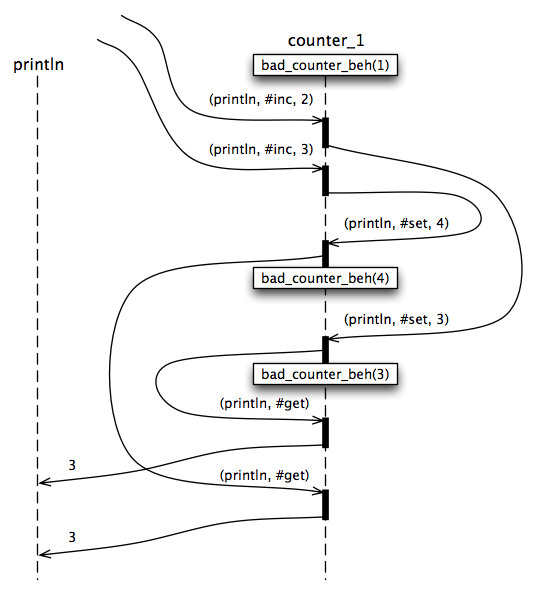
Separating the state-change in handling #set from the delegated reply to the customer may allow another request to affect the counter before the delegated #get is processed. This cannot lead to an inconsistency, since all the updates are correctly applied, but the results could be confusing. The value in the reply might not be the same as the value set.
Separating the computation of the new value in handling #inc from the delegated state-update can lead to an inconsistency (see Figure 4) in the value of the counter. The effects of any messages processed before the delegated #set will be overwritten by the computed value. This is a classic “race condition“. The problem was avoided in the original implementation by performing the state change and sending the reply message in the same request handler.
Conclusion
We have unpacked the Actor computational model and examined the “Send”, “Create” and “Become” primitives individually. The “Send” primitive is used to initiate work in the system. The in-flight (not yet delivered) messages in a system represent work to be done. The “Create” primitive is used to evolve the configuration of the system. Each actor created represents a capability to perform a certain kind of work. Since actor creation is cheap, it can be used to represent the state of an evolving computation. The “Become” primitive is used to change the state of an actor, or equivalently its behavior in response to messages. This allows the actor’s behavior/state to change over time based on messages that it receives and processes. Together these primitives form the basis of a powerful and elegant model for safe, efficient concurrent computation.
References
- [1]
- C. Hewitt. Viewing Control Structures as Patterns of Passing Messages. Journal of Artificial Intelligence, 8(3):323-364, 1977.
- [2]
- G. Agha. Actors: A Model of Concurrent Computation in Distributed Systems. MIT Press, Cambridge, Mass., 1986.
Tags: actor, asynchronous, capability, consistency, iteration, message-passing, primitive, recursion
That was a really interesting post, I enjoyed reading it. You are dead right!
I saw your presentation at InfoQ. Very interesting.
What isn’t clear to me is what language you are using. And is it available to play with.
Also, one tip: If I hadn’t seen the presentation, I wouldn’t have known that your code here uses backslash for lambda. You might want to put a note in the first blog entry. That is a language issue, I realize, but the code is somewhat readable without knowing all the details of the language, to one familiar with lambda notation.
Ach! I apologize. I went to the About page and it answered my question.
[…] Actor Model, on the other hand, takes an object-oriented approach. Each actor interprets messages (like method […]
[…] provides a solid foundation on which we will build a simple implementation of the Actor primitives (CREATE, SEND and BECOME). Encapsulated types and first-class environments help express Actor […]
[…] and designate a new behavior for handling future messages. Thus we have shown how all three actor primitives can be implemented within the JavaScript run-time […]
[…] In part 7 we will convert sequential block execution to proper parallel execution. We will also introduce transactions and exception handling. For more discussion of actor primitive semantics, see “Deconstructing the Actor Model“. […]